
įrom the figure, ∠3 and ∠4 are not adjacent but they make a Supplementary Angle if their sum is 180 0. They can be different Angles, only their sum should be 180 0.

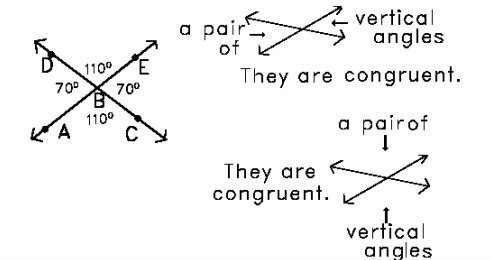
įrom the figure, we can say that ∠1 + ∠2 = 180 °īut it is not necessary that the two Supplementary Angles are always adjacent to each other. Here the Supplementary meaning is one Angle is supplemented to another Angle to make a sum of 180 0. When the sum of the measure of two Angles is 180 0, then the pair of Angles is said to be Supplementary Angles. įigure given below is a Complementary Angle example 27 + 63 = 9 0 o. They can be different Angles, only their sum should be 90 0. This is an example of a Complementary Angles example.īut it is not necessary that the two Complementary Angles are always adjacent to each other. In Complementary Angles one Angle is a complement of the other making a sum of 90 0 or you can say forming a right Angle.įrom the figure, we can say that ∠ABC + ∠CBD = 50 + 40 = 9 0 o. When the sum of the measure of two Angles is 90 0, then the pair of Angles is said to be Complementary Angles. In this session, we will be learning Complementary and Supplementary Angles in detail. Linear Pairs: linear pairs of Angles are adjacent to each other and have a common vertex and scissors is an excellent example to explain linear pair of Angles. Vertically Opposite Angles: vertically opposite Angles are equal to each other and are located opposite from a common vertex i.e, starting point or origin point. Simply explained, two pizza slices that are side by side in a box are considered to be adjacent to each other. Supplementary Angles: even if two Angles are not adjacent to each other or are not on the same line, but they sum up to result in 180 degrees, we call them Supplementary Angles.Īdjacent Angles: if two Angles have a common side or an arm or a vortex i.e, point of origin of the ray, we call the Angles, adjacent Angles. They are as follows:Ĭomplementary Angles: if two Angles are adjacent to each other or on the same line and the sum of a pair of Angles is 90 degrees, we call them complementary Angles as they complement each other to make the sum equal to 90 degrees.

There are more types of Angles on the basis of the pairs of Angles. So, the value of a reflex Angle ranges from 180 degrees to 360 degrees. Reflex Angle: if an Angle measures less than 360 degrees but greater than 180 degrees, then it is known as a reflex Angle. All the Angles in a square and a rectAngle are right Angles i.e, are equal to 90 degrees. If this right Angle is present in a triAngle, we call the triAngle a right-Angled triAngle. Right Angle: if an Angle measures exactly 90 degrees, then it is called a right Angle. So, the value of an obtuse Angle ranges from 90 degrees to 180 degrees. Obtuse Angle: An Angle measuring more than 90 degrees but less than 180 degrees is called an obtuse Angle. So, the value of an acute Angle varies from 0 to 90 degrees. Angles are Classified According to Their Sizes as FollowsĪcute Angle: An Angle measuring less than 90 degrees is called an acute Angle. Angles are commonly measured in terms of degree. B is the point of intersection called the vertex and AB and BC are the sides of the Angle. An Angle is denoted by the symbol ∠.įrom the figure, ∠ABC is an Angle. When two lines intersect they form four Angles at the point of intersection. Various parts of an angle are vertex, arms, interior, and exterior angles.
We know that two lines having a common vertex form an angle. An angle that measures 90 0 is a Complementary angle and whose measure is 180 0 is a Supplementary Angle. Complementary and Supplementary Angles are the two types of angles based on their measures.


 0 kommentar(er)
0 kommentar(er)
